Desde la antigüedad más remota, los juegos de azar y de suerte han interesado al hombre; se sabe que el uso de las tabas es tan viejo como la humanidad misma y parece ser el antecesor de los dados y de la ruleta. El primer dado conocido es de arcilla cubierta de cuero, fue encontrado al norte de Irak y data de principios del tercer milenio a.C.
Los griegos, que tenían una diosa de la suerte llamada Tique, de origen egipcio construyeron dados poliédricos que recordaban los sólidos platónicos, algunos se conservan en el museo del Louvre, en París.
Según la Biblia, unos 1000 años a.C., los israelitas eligieron un rey por sorteo (Samuel 10:20-24).
Pero el cálculo de probabilidades entró muy lentamente a formar parte del campo de las matemáticas. El primer documento conocido donde se analizan los juegos de azar en forma sistemática es el Liber de ludo aleae (Manual sobre juegos de azar), escrito por Gerolamo Cardano alrededor de 1550, pero publicado unos cien años después de su muerte. El gran Galileo también se interesó por los juegos de azar y escribió un folleto titulado Sopra le scopere dei dadi (Descubrimientos sobre los juegos con dados) publicado en 1718.
A continuación, veremos algunos de los problemas concretos y prácticos a partir de los cuales se fue creando poco a poco el modelo matemático que es hoy el cálculo de probabilidades.
El problema del duque de Toscana (1560)
El duque de Toscana fue un jugador empedernido, y había observado que en un juego en el que se tiran tres dados y se suman los puntos, el 10 aparecía más veces que el 9. Sin embargo, según el duque, ambos números se pueden obtener de las seis maneras que se listan.
1+2+6=9 \ 1+3+6=10
1+3+5=9 \ 1+4+5=10
1+4+4=9 \ 2+2+6=10
2+2+5=9 \ 2+3+5=10
2+3+4=9 \ 2+4+4=10
3+3+3=9 \ 3+3+4=10
Cardano fue consultado y estudió el problema, pero no encontró respuesta satisfactoria. Fue Galileo quien encontró la solución 50 años más tarde; para ello contó todos los casos posibles y, por primera vez, presentó los datos en tablas de distribución, como la siguiente, que corresponde al problema anterior:
El 9 se obtiene de las siguientes maneras: (6,1,2), (6,2,1), (5,1,3), (5,2,2), (5,3,1), (4,1,4), . . . ,(1,6,2). En total, hay 25 maneras de obtener 9. El 10 se obtiene de 27 maneras distintas: (6,1,3), (6,2,2), (6,3,1), (5,1,4), (5,2,3),(5,3,2),...
Por lo tanto, es normal que el 10 ocurra con más frecuencia que el 9.
| Suma de los puntos con 3 dados | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Número de maneras de obtenerlos | 1 | 3 | 6 | 10 | 15 | 21 | 25 | 27 | 27 | 25 | 21 | 15 | 10 | 6 | 3 | 1 |
Los problemas del Caballero de Méré (1650)
Antoine de Gambaud, Chevalier de Méré, fue jugador, hombre de letras y cortesano muy conocido en la corte del rey Luis XIV de Francia. Su primer problema es parecido al del duque de Toscana: ¿Cómo puede ser que el 11 ocurra más veces que el 12 cuando se tiran tres dados si ambos números se pueden formar de seis maneras distintas? El Caballero de Méré consultó a su amigo Blaise Pascal quien, mediante ese problema, empezó a interesarse por las probabilidades y resolvió este mismo problema (utilizó el mismo método que Galileo) y muchos más.
Para el segundo problema del Caballero de Méré, Pascal pidió la opinión de Fermat y escribió (1654): "El Caballero de Méré es muy talentoso, pero no es matemático y eso, usted lo sabe bien, es un gran defecto". Este es el problema:
Dos personas, A y B, participan en un juego donde las dos tienen la misma probabilidad de ganar (o sea 1/2; por ejemplo, lanzando una moneda). El primero que gane cinco veces cobra el premio de 4,200 francos franceses. Desgraciadamente, después de lanzar la moneda siete veces hay que suspender la contienda; en ese momento A ha ganado 4 veces y B ha ganado 3 veces.
¿Cómo tiene que dividirse el premio entre los dos jugadores? Se propusieron varias soluciones:
- Dividir el premio proporcionalmente a 4 y 3, puesto que el torneo terminó de esa forma; o sea, A cobraría 2,400 FF y B cobraría 1,800 FF.
- Dividir el premio proporcionalmente a (5-3) y (5-4), ósea 2 y 1.
En ese caso, A cobraría 2,800 FF Y B cobraría 1,400 FF.
Ninguna de las soluciones presentadas convencía a los jugadores, hasta que Pascal y Fermat propusieron un esquema que tomaba en cuenta el hecho de que A tenía la ventaja de haber ganado ya 4 partidas. El análisis que hicieron inició el estudio de la "probabilidad condicionada", y el método que usaron se aplica hoy a muchas situaciones que van desde los negocios hasta la medicina. Un diagrama de árbol facilita la representación visual del problema:
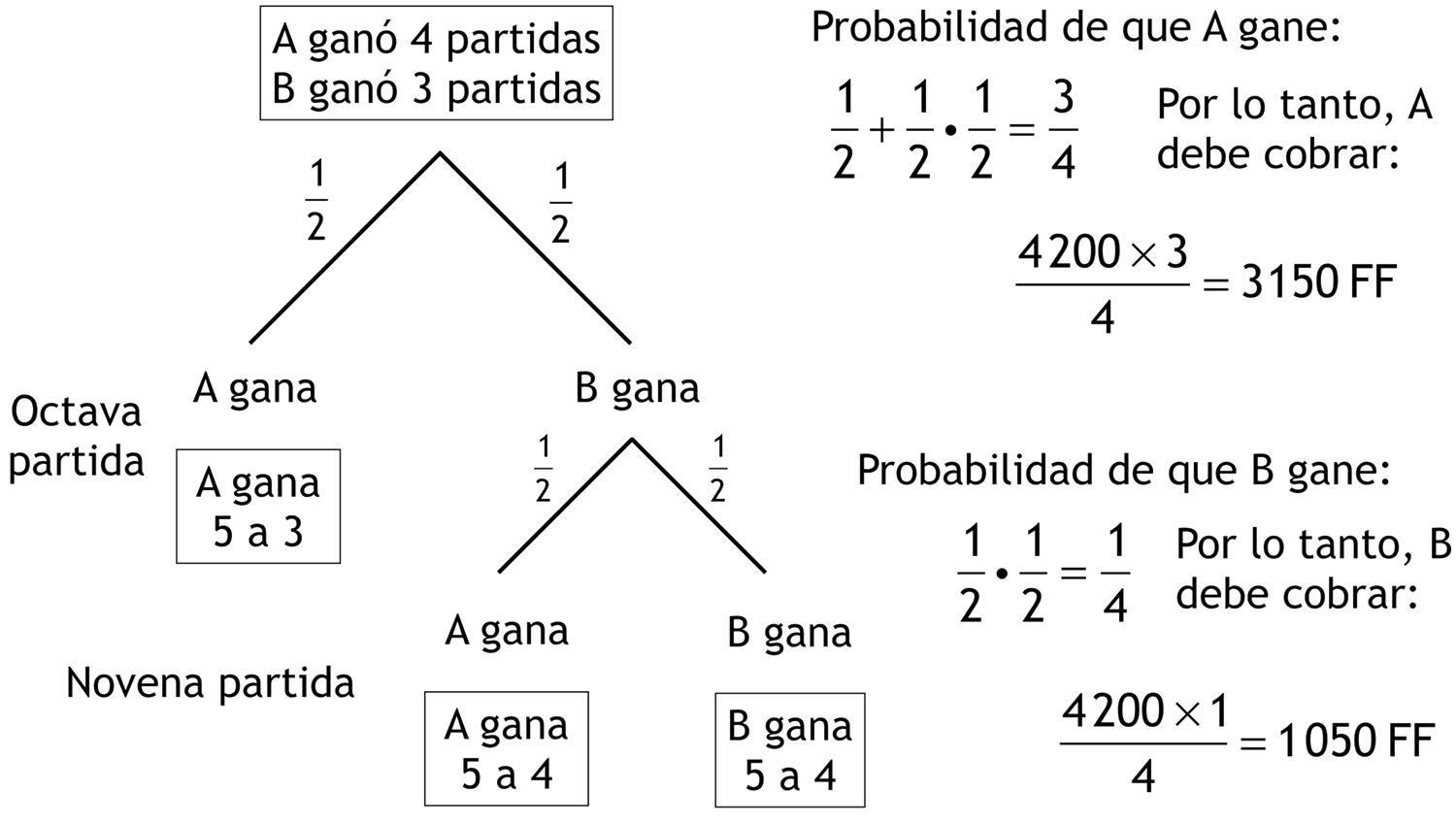
El error de d'Alembert (Siglo XVIII)
Jean Le Rond d' Alembert fue un famoso matemático francés del siglo XVIII; es también famoso por haberse equivocado en el siguiente problema que le fue planteado en 1754:
¿Cuál es la probabilidad de que salga cara por lo menos una vez cuando se lanzan dos monedas? (cara-cruz equivale a águila-sol)
D'Alembert analizó el problema diciendo que existían tres posibilidades:
- Cara en el primer lanzamiento
- Cara en el segundo lanzamiento
- Ninguna cara
Como hay 3 casos posibles y dos favorables, la probabilidad buscada es 2/3.
El análisis correcto es observar que hay 4 casos posibles: cara-cara, cara-cruz, cruz-cara, cruz-cruz; en 3 de estos casos ocurre cara por lo menos una vez, la probabilidad buscada es por lo tanto 3/4.
La paradoja de San Petersburgo (Siglo XVIII)
En 1725, Daniel y Nicolás Bernoulli enseñaban matemáticas en la academia (que Pedro el Grande de Rusia acababa de crear) de la ciudad de San Petersburgo, Nicolás había propuesto en los Commentarii de dicha academia el problema siguiente, conocido como la paradoja de San Petersburgo.
El juego consiste en lanzar una moneda hasta que salga cara.
- Si sale cara la primera vez, Daniel paga una corona a Nicolás.
- Si sale cruz primero y cara en el segundo lanzamiento (Cr,C), Daniel paga 2 coronas.
- Si sale cara por primera vez en el tercer lanzamiento (Cr,Cr,C) Daniel paga 4 coronas.
- Si la sucesión es Cr,Cr,Cr,C, Daniel paga 8 coronas.
- etc...
Si la sucesión es Cr,Cr,Cr, . . . , Cr, C, con n lanzamientos, Daniel paga 2^(n-1) coronas.
En otras palabras,
- la probabilidad de que Nicolás cobre 1 corona es 1/2
- la probabilidad de que Nicolás cobre 2 coronas es 1/4
- la probabilidad de que Nicolás cobre 4 coronas es 1/8
- etc...
El problema es: ¿Cuánto tiene que pagar Nicolás a Daniel para jugar si quiere que el juego sea equitativo?
Lo que puede ganar Nicolás (su esperanza matemática) es:
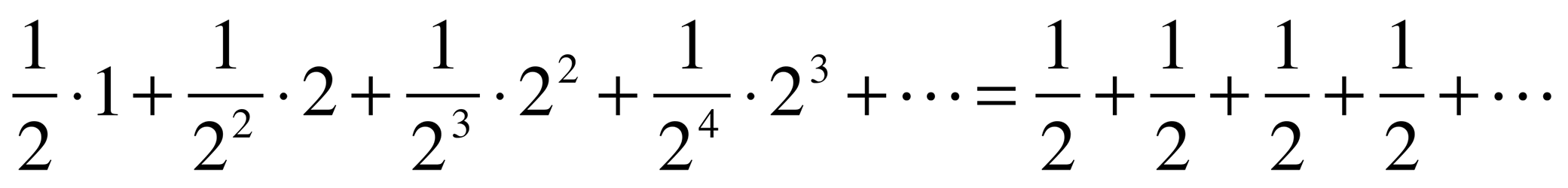
una suma infinita; por lo tanto, en teoría, tendría que pagar una suma infinita de dinero para que el juego sea equitativo. Sin embargo, el sentido común sugiere
que solo hay que pagar una pequeña cantidad.
Georges Louis Leclerc, conde de Buffon, un conocido naturalista francés (1707-1788), hizo una prueba empírica: contrató a un niño para que lanzara una moneda al
aire muchas veces (no había entonces computadoras para hacer experimentos simulados). El niño lanzó la moneda 2,084 veces y encontró que Nicolás tendría que pagar a
Daniel 10,057 coronas, un promedio de 5 coronas por partida, no la suma infinita dada por la teoría (en el experimento simulado, se pagó, en 1,061 partidas, 1 corona; en
494 partidas, se pagaron 2 coronas, etc. ...).
El conde de Buffon fue el primero en subrayar la importancia de la verificación de una teoría con experimentos reales.
Se ha tratado de explicar la paradoja de San Petersburgo de varias maneras. Daniel Bernoulli inventó el principio de "Esperanza Moral", y describió una nueva
función que denominó “función utilitaria”: el valor de una pequeña cantidad de dinero no es el mismo para un rico que para un pobre (definió la “esperanza moral" como
la esperanza matemática del logaritmo de la fortuna).
Otra explicación consiste en decir que, siendo finita la fortuna de Nicolás, es imposible que éste pueda pagarle a Daniel si la cara tarda mucho en salir. Dicho de
otra manera, la “esperanza matemática infinita” se explica por el hecho de que existe la posibilidad, aunque muy remota, de ganar una suma enorme (infinita) si ocurre una
larga racha de caras.
En resumen, la paradoja de San Petersburgo es un caso particular del problema general de "doblar" la apuesta en los juegos de azar; sistema con el cual en
teoría no se puede perder (puesto que en algún momento saldrá la cara); pero en el que se pierde siempre en la práctica, ya que la cantidad de dinero de que dispone el
jugador es siempre finita y casi siempre inferior a la de la banca. Para asegurar más todavía su probabilidad de no perder, los casinos fijan una cantidad máxima para todas las apuestas.
El conocido matemático suizo Gabriel Cramer (1704-1752) explica que la fortuna de la banca, aunque puede ser muy grande, es siempre limitada. Suponiendo que el capital
de la banca sea de $ 224, el jugador tiene la probabilidad 1/(2n) de recibir $ 2n-1 cuando n es menor que 25, pero después solo podrá
recibir $ 224. Su esperanza matemática es entonces $ 13, lo cual es bastante razonable. Este es el cálculo que hacía Cramer:
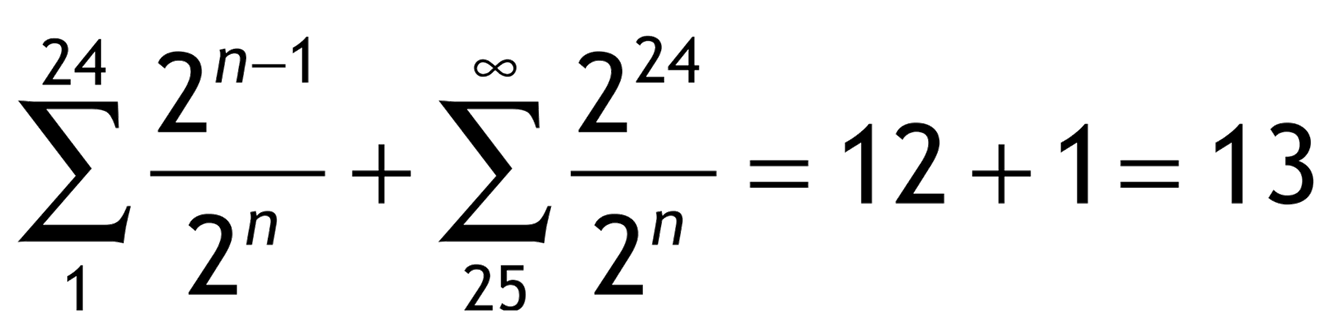
Cita textual de: PERERO, Mariano. Historias e historia de las matemáticas. Editorial iberoamérica, México. 1994, pp. 88-94.
